SUSCTF-tttree2

SUSCTF-REVER-tttree

0X1准备步骤

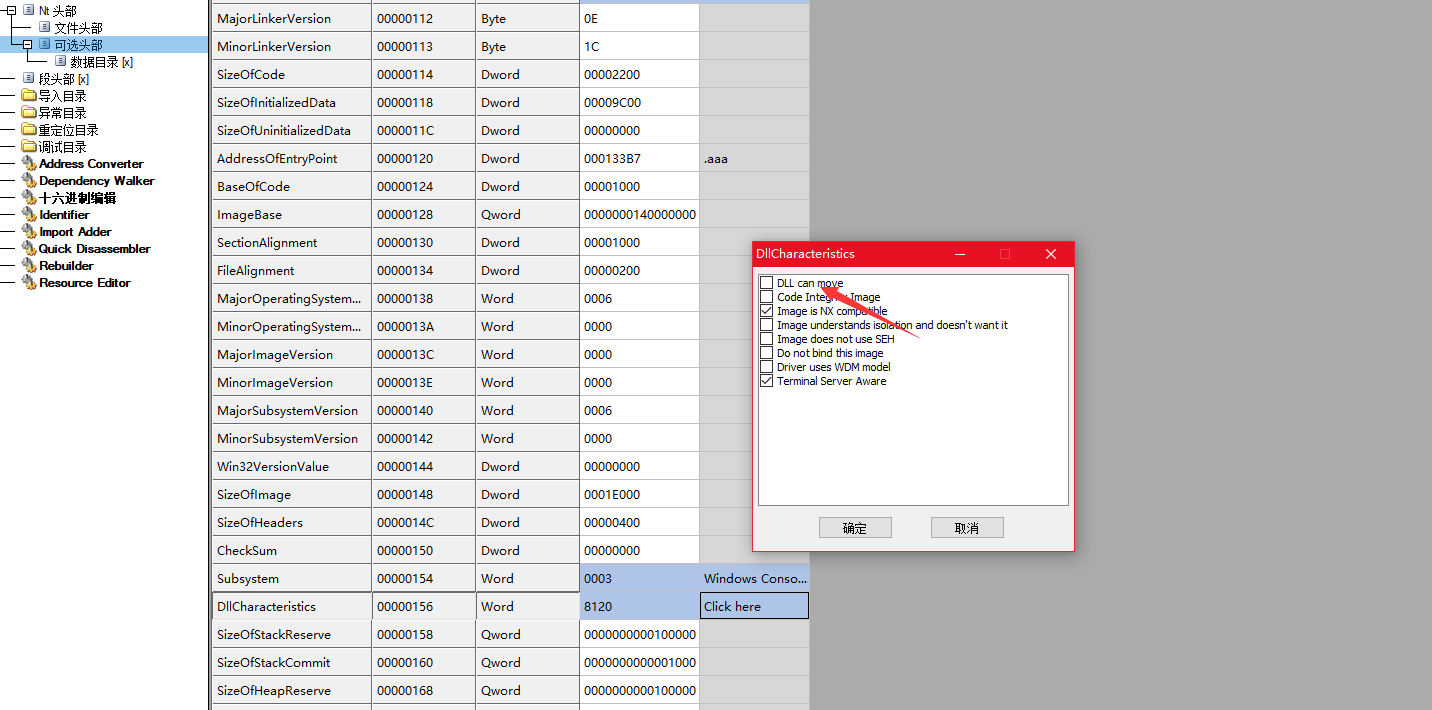
把文件拉进CFF Explorer_CN 取消 DLL can move 这样程序每次加载，不会改变基址 方便下断

0x2动调分析

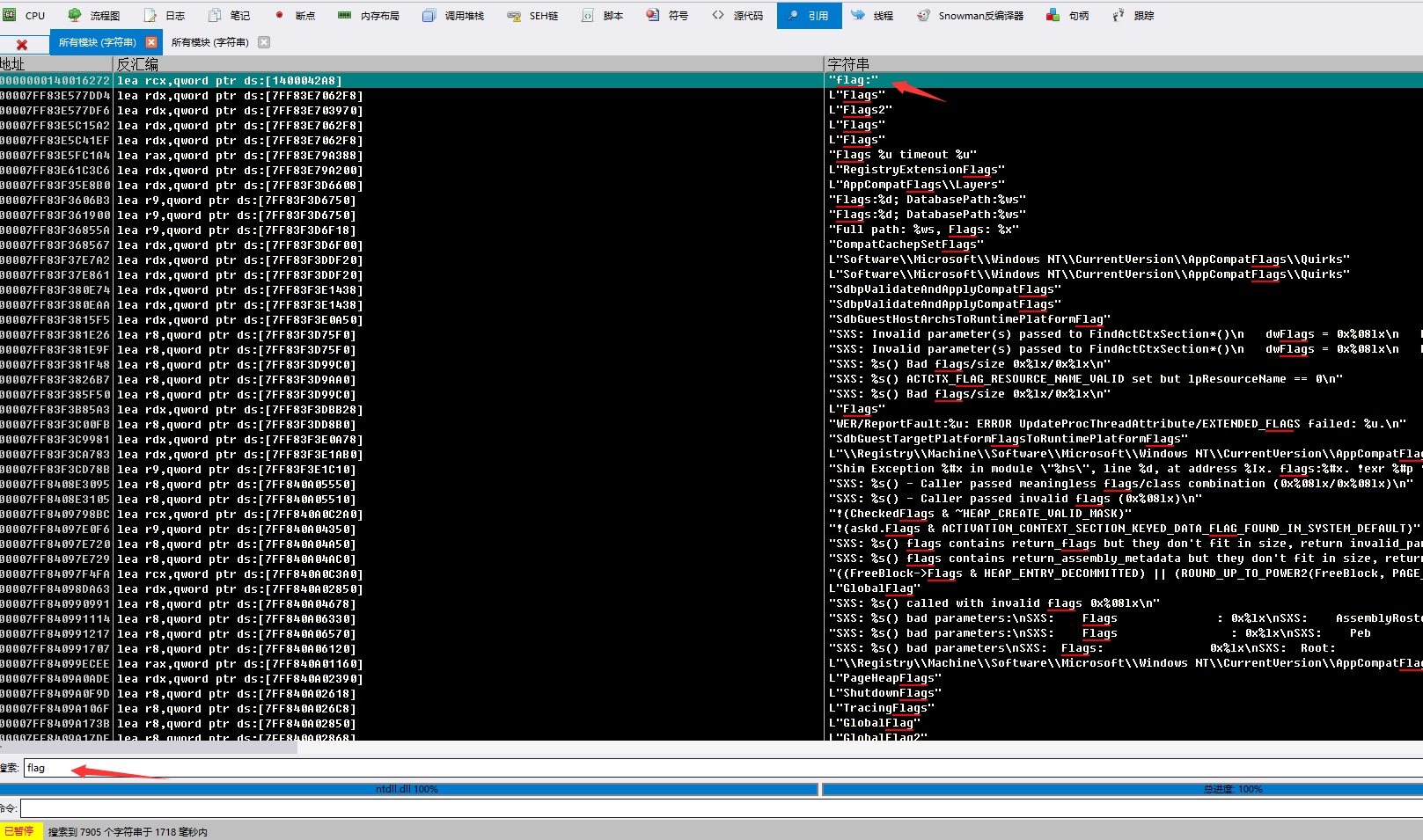
搜索关键字符串跳转下断

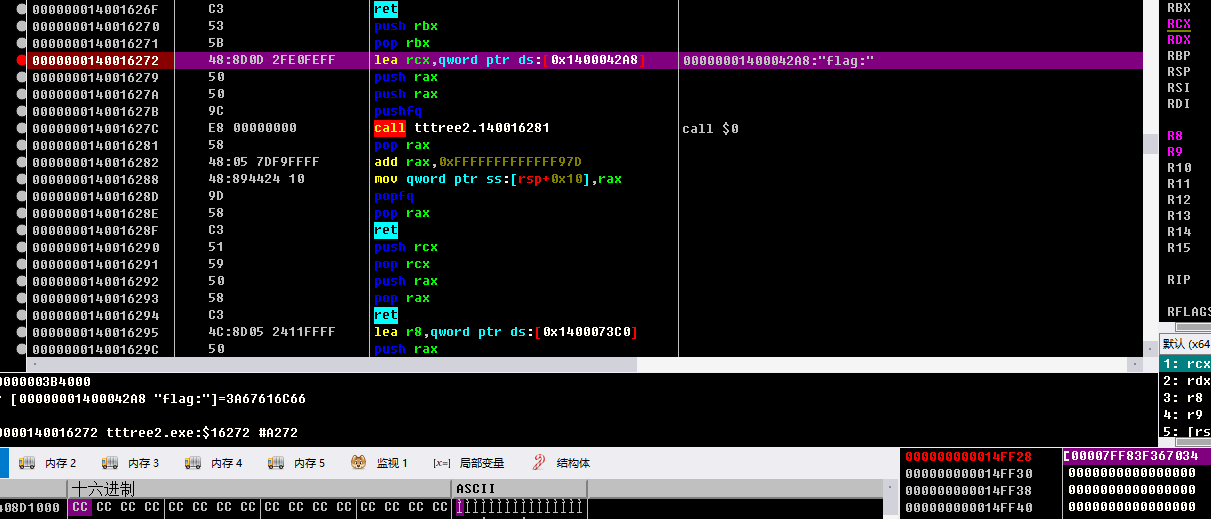
然后一路F8就完事，一直到需要你输入

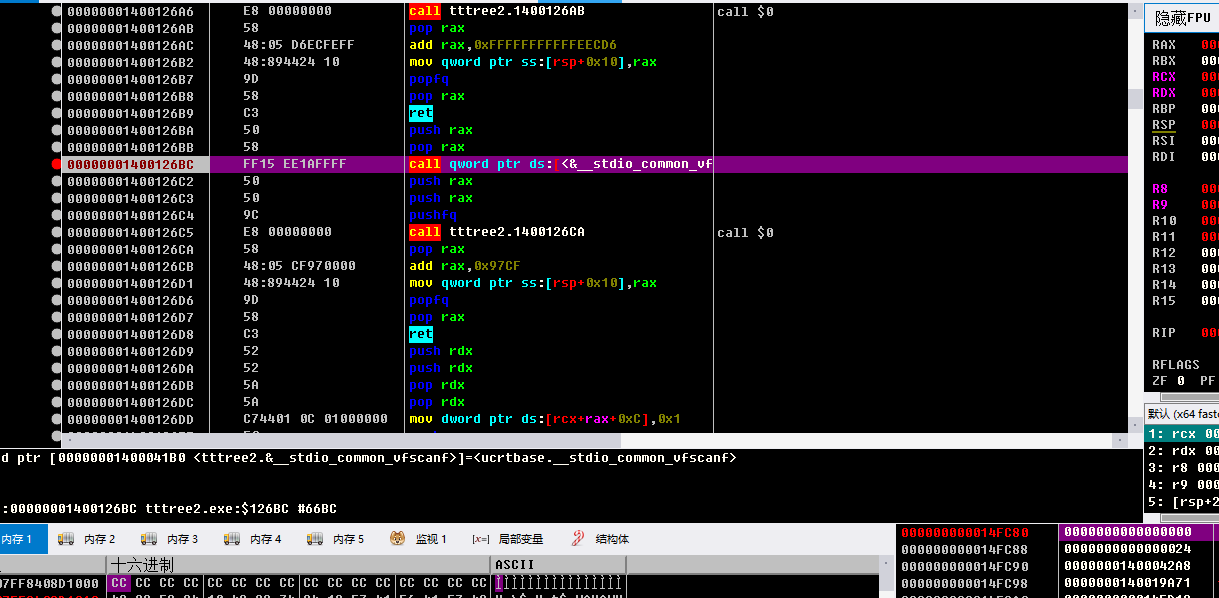
到达位置，直接下断，下次重新来就不需要再找字符串下断

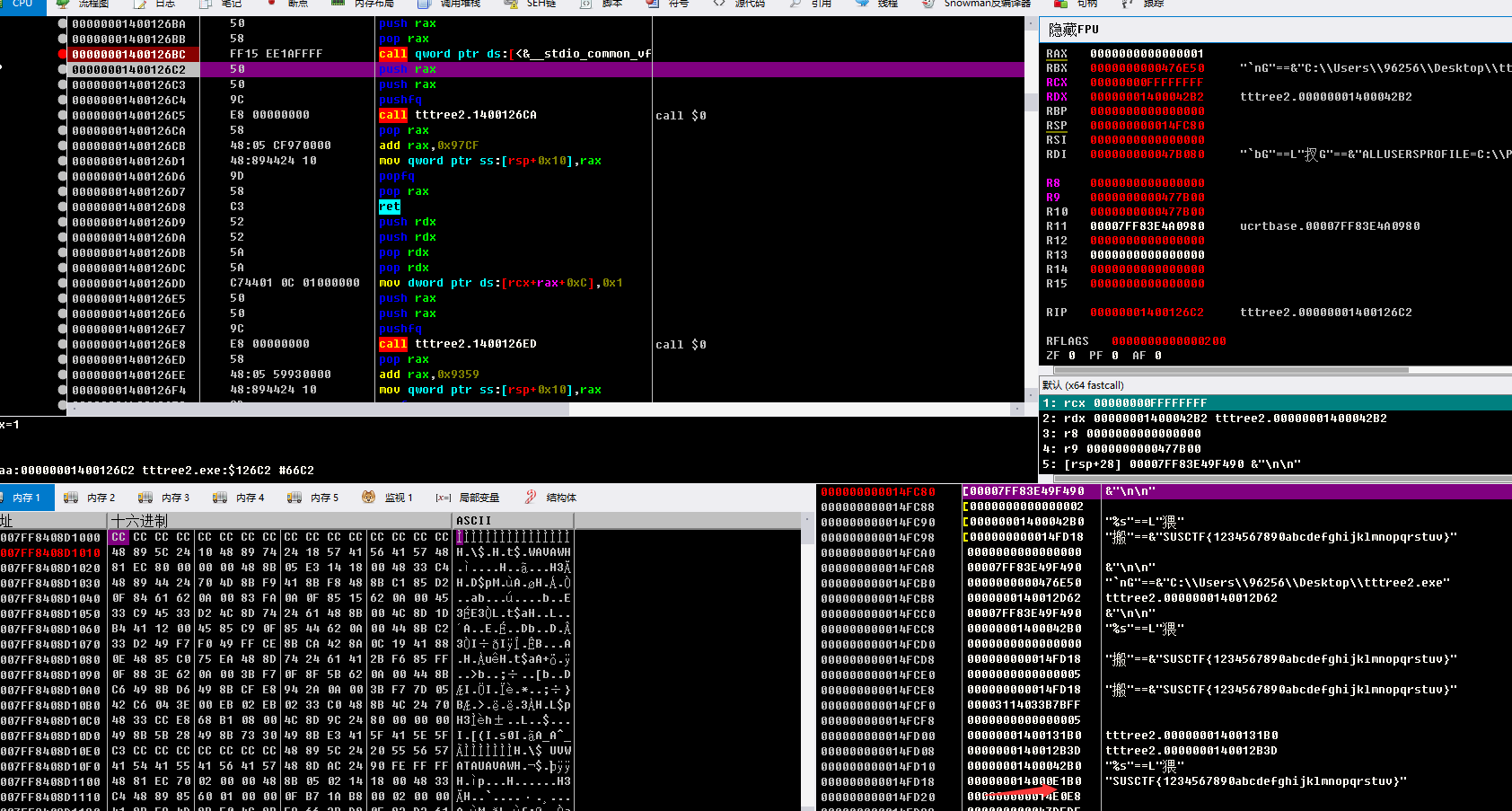
输入字符串 可以看见堆栈右下角 地址存储着我们输入的假flag

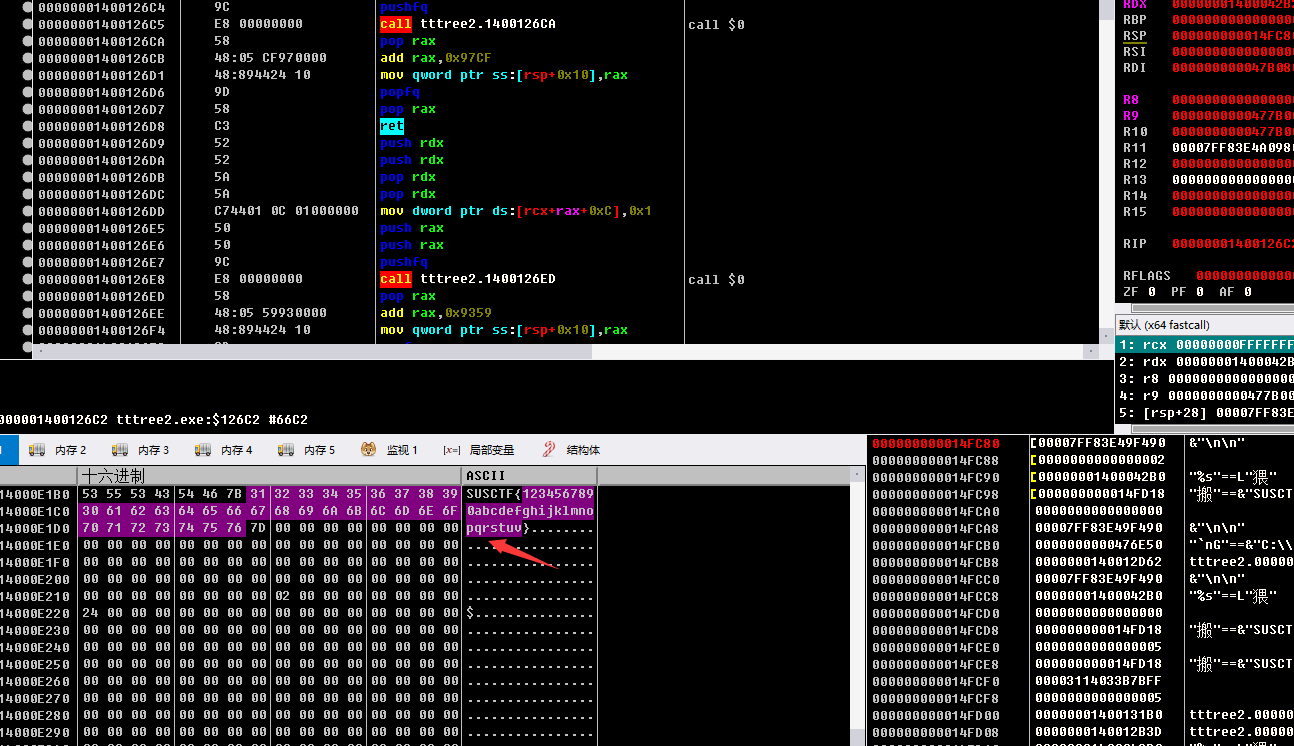
内存跳转过去 下硬件访问断点

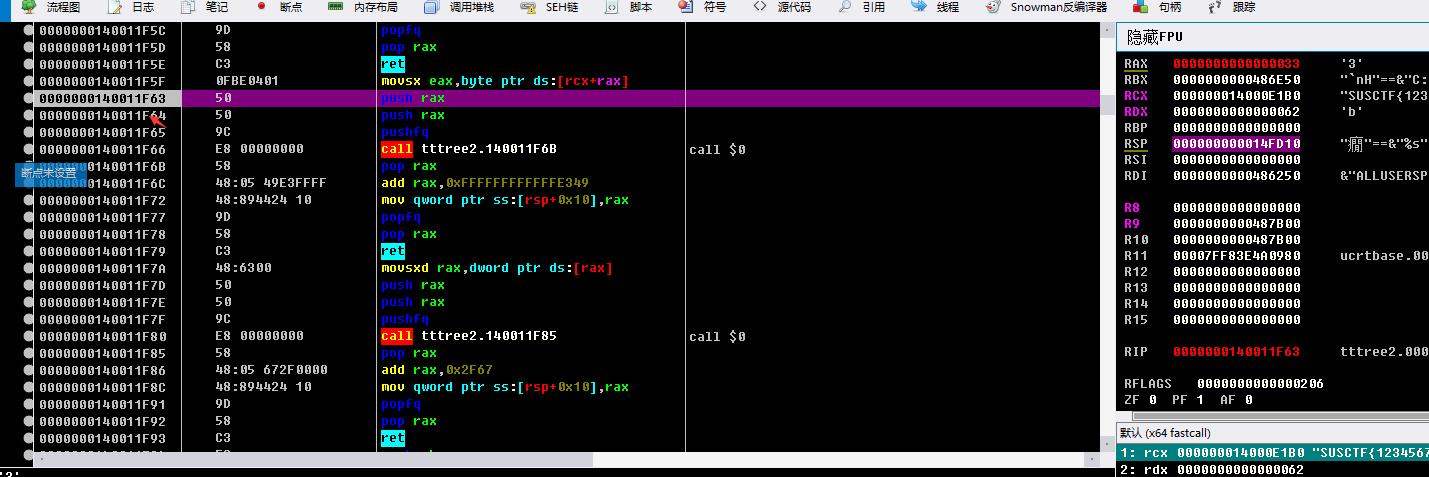
可以看见140011F5F 这个地址每次读取一位我们的flag

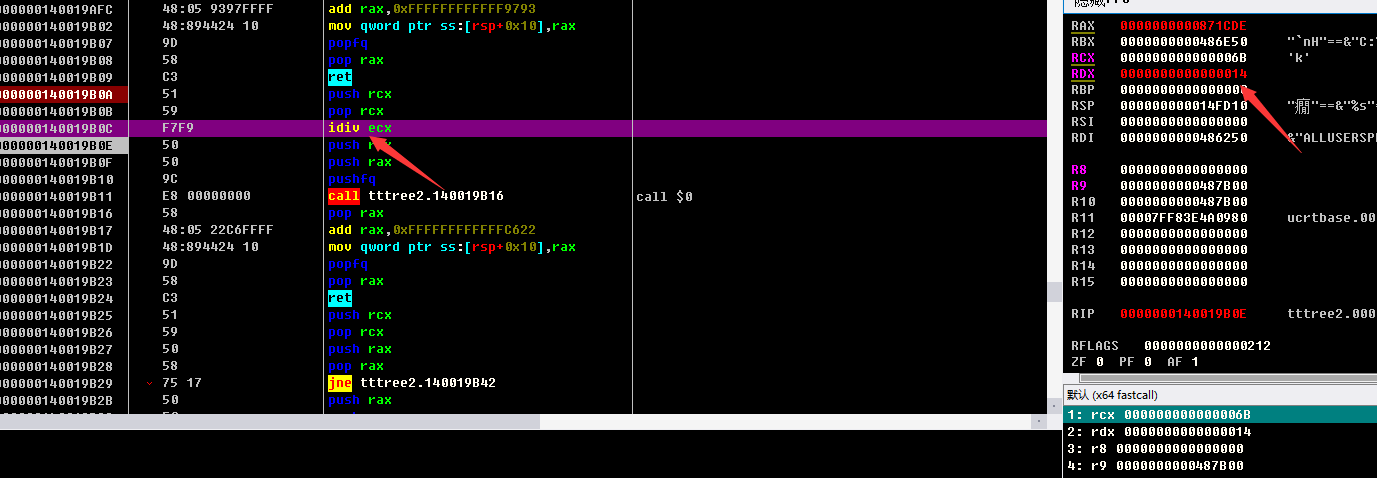
往下跟发现 在idiv 这里每次计算出来的值放入 RDX 可以在 idiv 下面地址下断，一直运行提取里面的值

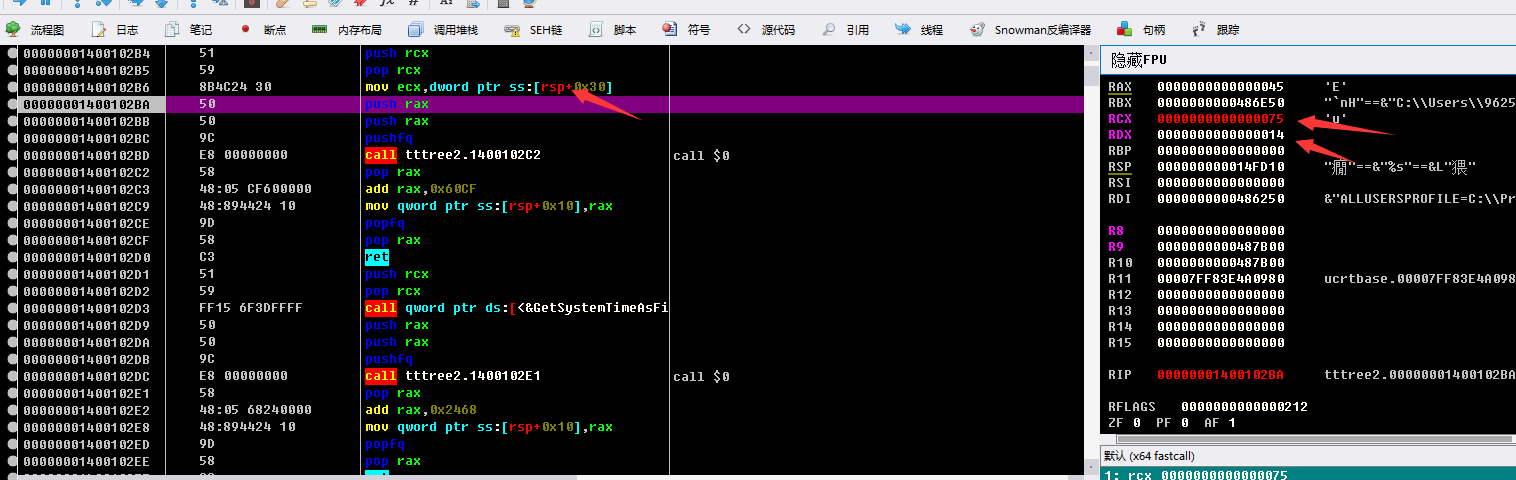
每次给RCX赋值的地方 后面一直循环发现 RCX的值 = RDX的值 + 97

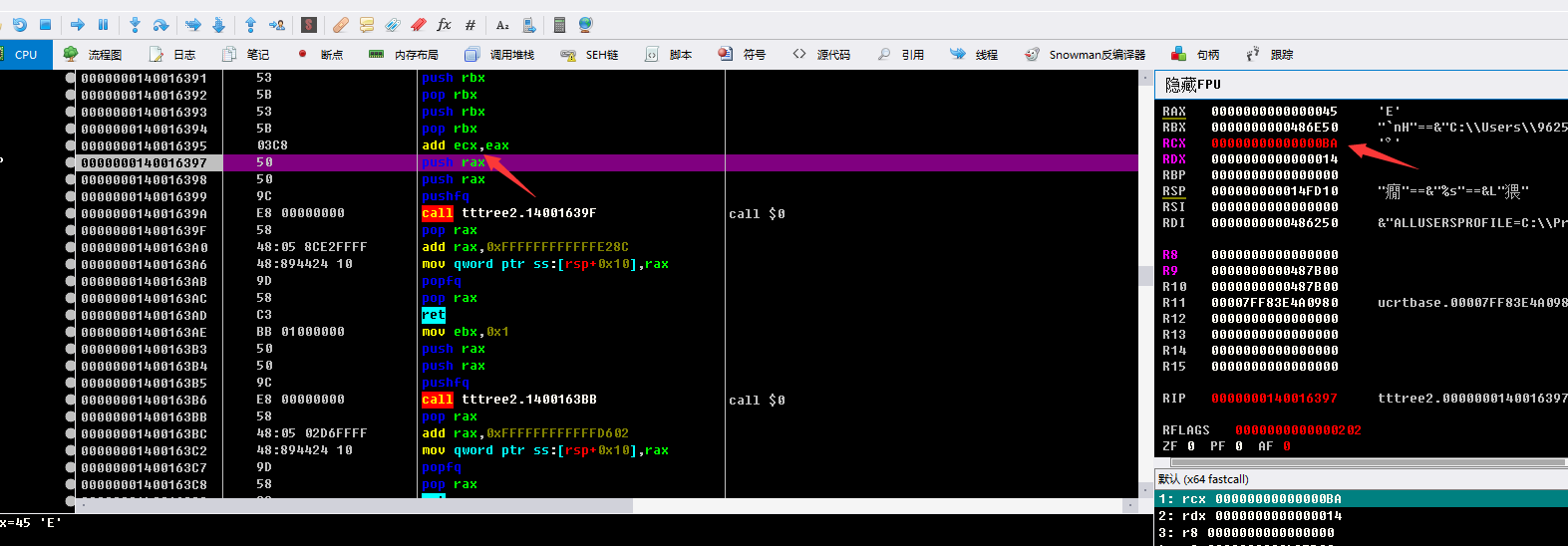
然后将我们的flag值 与 RCX的值相加

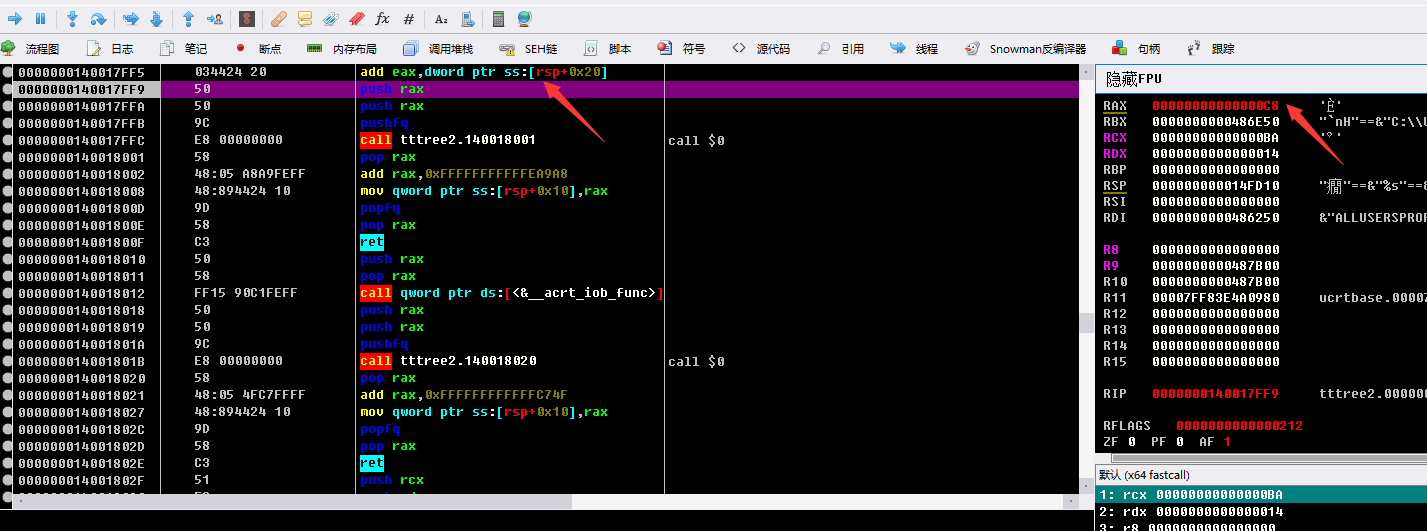
然后还会再加我们flag值的索引 ，可以想成每次加 i i是从0开始

0x3加密flag 逆推

先提取出 每次RDX的值

key = [0x60, 0x46, 0x62, 0x03, 0x16, 0x19, 0x1E, 0x12, 0x4D, 0x51, 0x05, 0x25, 0x38, 0x2F, 0x14, 0x4F,0x5B, 0x2D, 0x4C, 0x26, 0x5A, 0x0F, 0x04, 0x07, 0x5F, 0x1D, 0x48, 0x1F, 0x67, 0x44, 0x3B, 0x37]

加密算法为 flag + key + 97 + i

逆推回去只需要将加密过后的flag flag = [enc_flag[ i ] - key[ i ] - 97 - i for i in range(len(enc_flag))] 就可以得到flag

def get_real_c(_index, enc_input):
    # 通过索引和enc_input得到原始input
    tmp = enc_input - 97 - key[_index] - _index
    return tmp

0x4再次动调分析

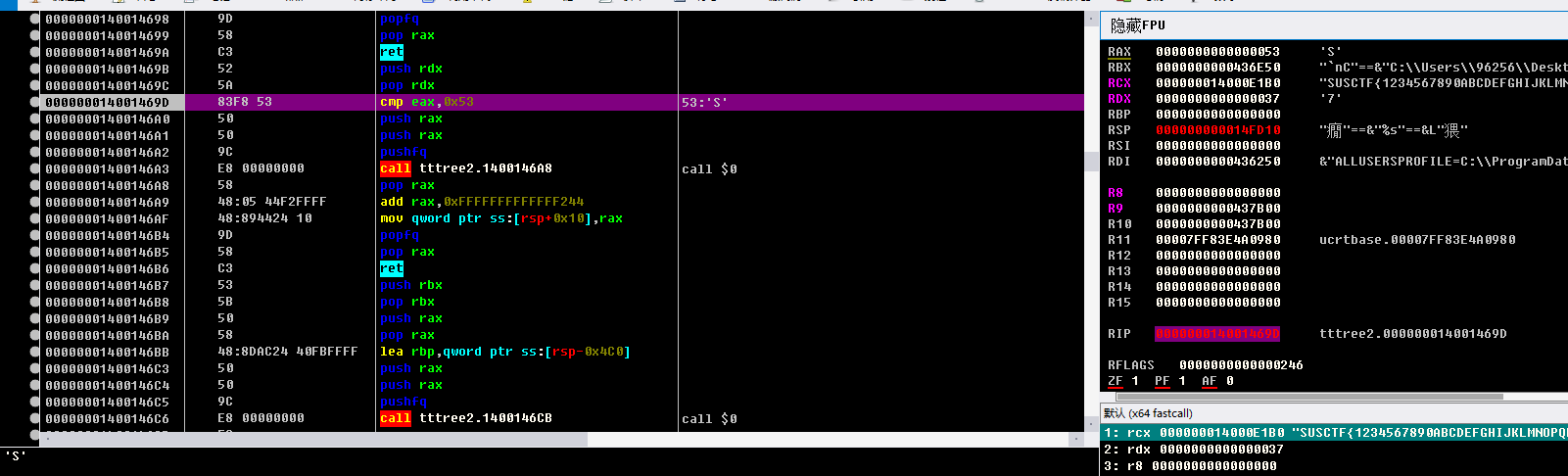
再往后走 发现这里才开始判断了SUSCTF{} 前面只是判断了{中间的值}

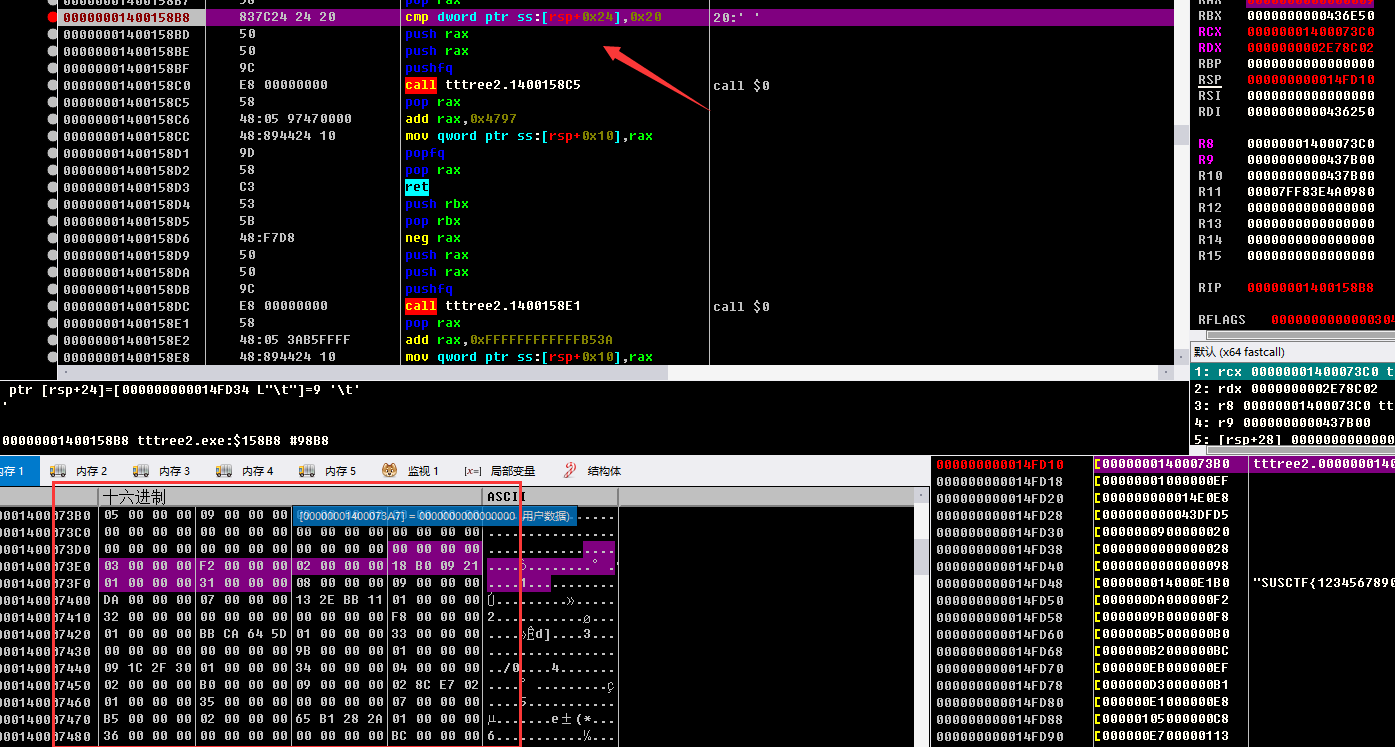
后面一直循环动调都会到这里判断节点个数 发现中间会往 1400073B0里放入这里，发现是一个长度为33的结构体数组

struct tree_node{
   0x00 DWORD 左孩子;               //左孩子 右兄弟表示二叉树里的代名词
   0x04 DWORD 右兄弟;
   0X08 DWORD enc_input;        //加密后的每一个字符
   0X0C DWORD 叶子个数;    //假设把此节点当做根节点，整个Tree的叶子个数
   0X10 DWORD 随机数;            //优先级
   0X14 DWORD  1;             
   0X18 DWORD input;         //输入的flag的每一个字符
}

总共有32个数组结构体 全部提取出来

				  输入加密后	 页子个数   优先级				我们的输入
00000000 00000013 000000F1 00000006 2109B018 00000001 00000030
0000000F 00000009 000000D9 00000018 11BB2E13 00000001 00000031
00000000 00000000 000000F7 00000001 5D64CABB 00000001 00000032
00000000 0000000B 0000009A 00000002 302F1C09 00000001 00000033
00000004 00000015 000000AF 00000020 02E78C02 00000001 00000034
00000000 00000000 000000B4 00000001 2A28B165 00000001 00000035
00000000 00000000 000000BB 00000001 6F018185 00000001 00000036
00000000 00000006 000000B1 00000002 1CF5A8D1 00000001 00000037
00000016 00000011 000000EE 0000000E 1532F368 00000001 00000038
00000000 00000000 000000F4 00000001 42367652 00000001 00000039
00000000 00000000 000000A0 00000001 7B50B157 00000001 00000030
00000007 00000000 000000C2 00000002 244FA941 00000001 00000031
00000000 00000000 000000D7 00000001 48CB7CCC 00000001 00000032
0000000C 00000014 000000CF 00000004 1950F130 00000001 00000032
00000008 00000012 000000B6 00000009 15561F1B 00000001 00000033
00000000 0000000A 000000F3 00000002 29F35383 00000001 00000034
00000001 00000020 00000101 0000000A 204017F9 00000001 00000035
0000000E 0000000D 000000D5 00000006 15686F99 00000001 00000036
00000010 0000001A 000000F6 00000005 274AD200 00000001 00000037
00000000 00000000 000000D3 00000001 650387E1 00000001 00000039
0000001B 00000019 00000130 0000001D 04C2B77D 00000001 00000061
00000017 00000000 000000E7 00000003 278451D6 00000001 00000062
00000000 00000018 000000DE 00000002 3F0318C0 00000001 00000063
00000000 00000000 000000E3 00000001 78E83012 00000001 00000064
00000000 0000001D 0000013D 00000002 0D00C42A 00000001 00000065
00000003 00000000 000000FD 00000002 537C7E9D 00000001 00000066
00000002 0000001E 0000012A 0000001A 0F8680AF 00000001 00000067
00000000 00000000 00000103 00000001 72A27C9F 00000001 00000068
00000000 00000000 0000014D 00000001 5C4909AF 00000001 00000069
00000000 00000000 0000012C 00000001 2FE974B3 00000001 0000006A
00000000 00000000 00000125 00000001 351BEA91 00000001 0000006B
0000001C 0000001F 00000123 00000003 2ADAD13B 00000001 0000006C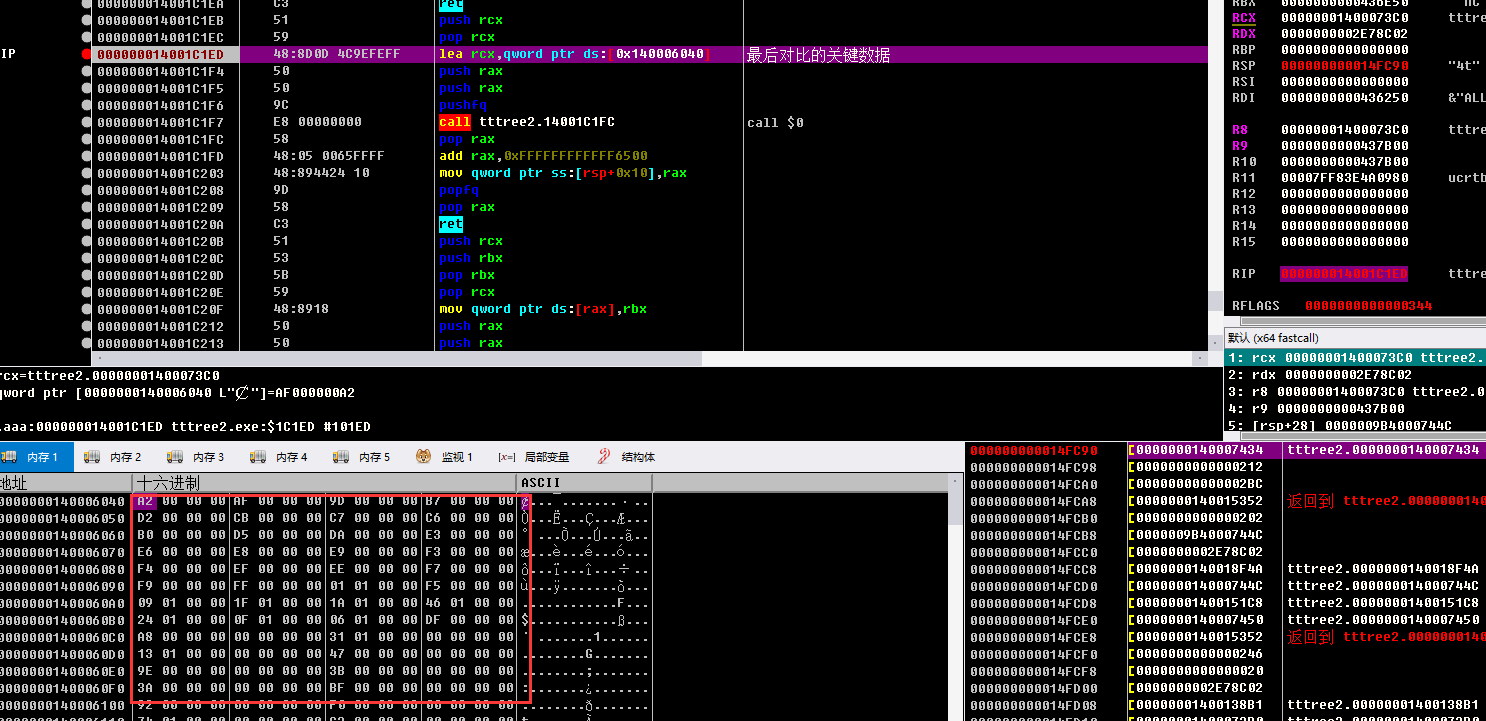

32个数组全部走出来后 提取了正确的加密后的flag 调试时可以发现为后序遍历二叉树

如何判断

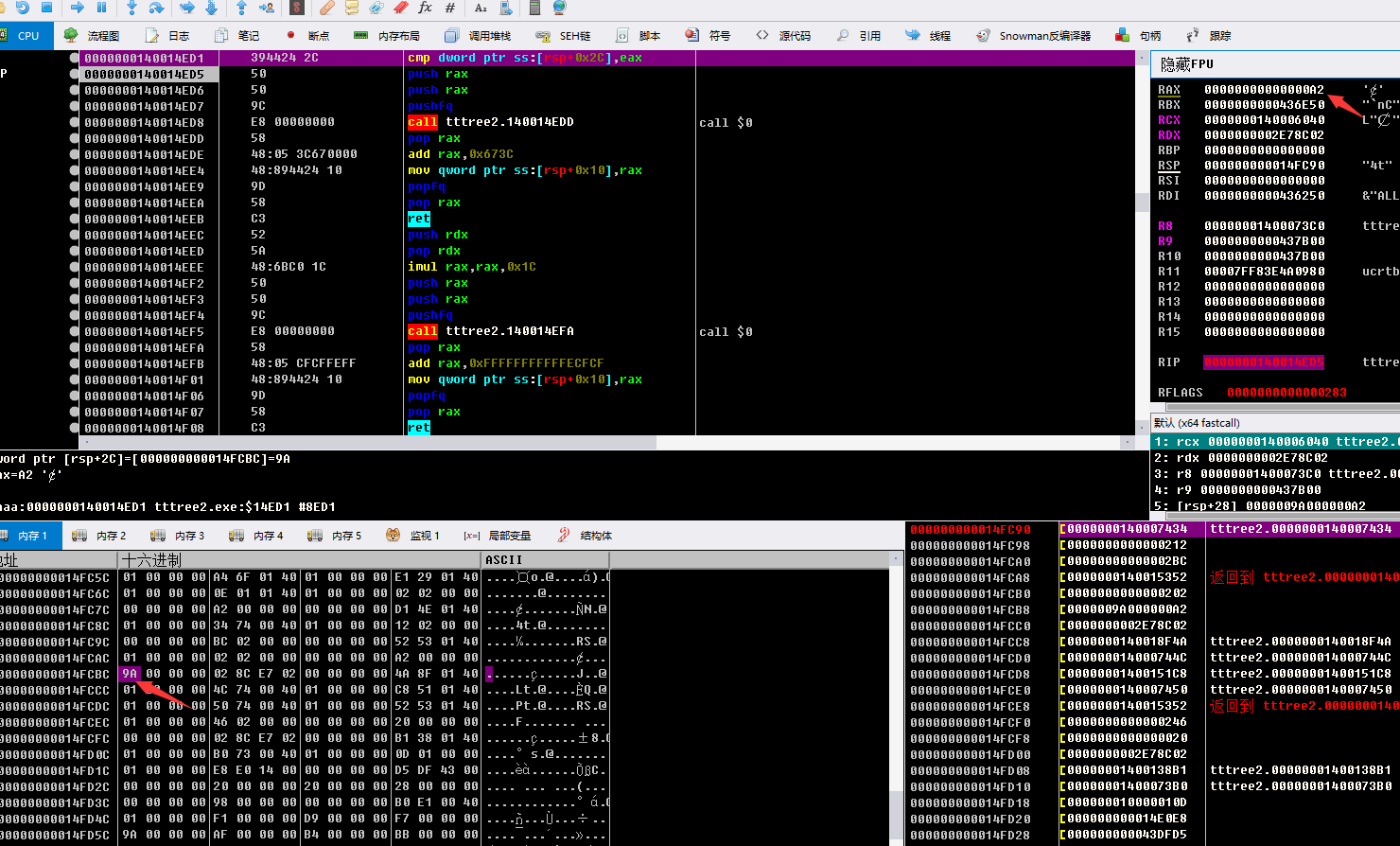
后面有对比 一个值为0xA2 是0x140006040里的第一个值 来判断出那个数组为最终判断的flag

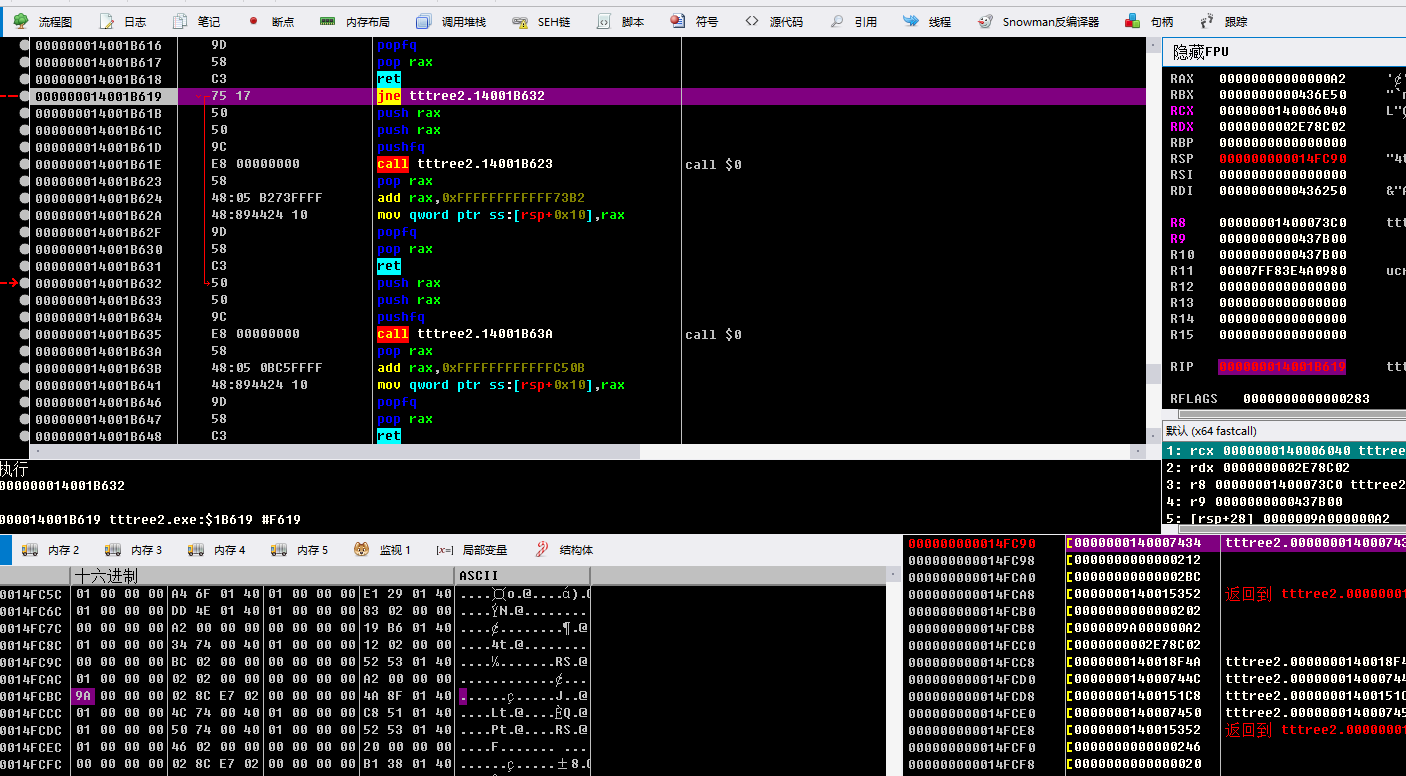
这里是关键判断 jne跳走直接结束了 改变 zf标志位 或者 jne 改成 je 继续动调

0x5构造二叉树

提取出正确的flag值，构造二叉树

encs = [0x00A2, 0x00AF, 0x009D, 0x00B7, 0x00D2, 0x00CB, 0x00C7, 0x00C6, 0x00B0, 0x00D5, 0x00DA, 0x00E3, 0x00E6, 0x00E8, 0x00E9, 0x00F3,0x00F4, 0x00EF, 0x00EE, 0x00F7, 0x00F9, 0x00FF, 0x0101, 0x00F5, 0x0109, 0x011F, 0x011A, 0x0146, 0x0124, 0x010F, 0x0106, 0x00DF]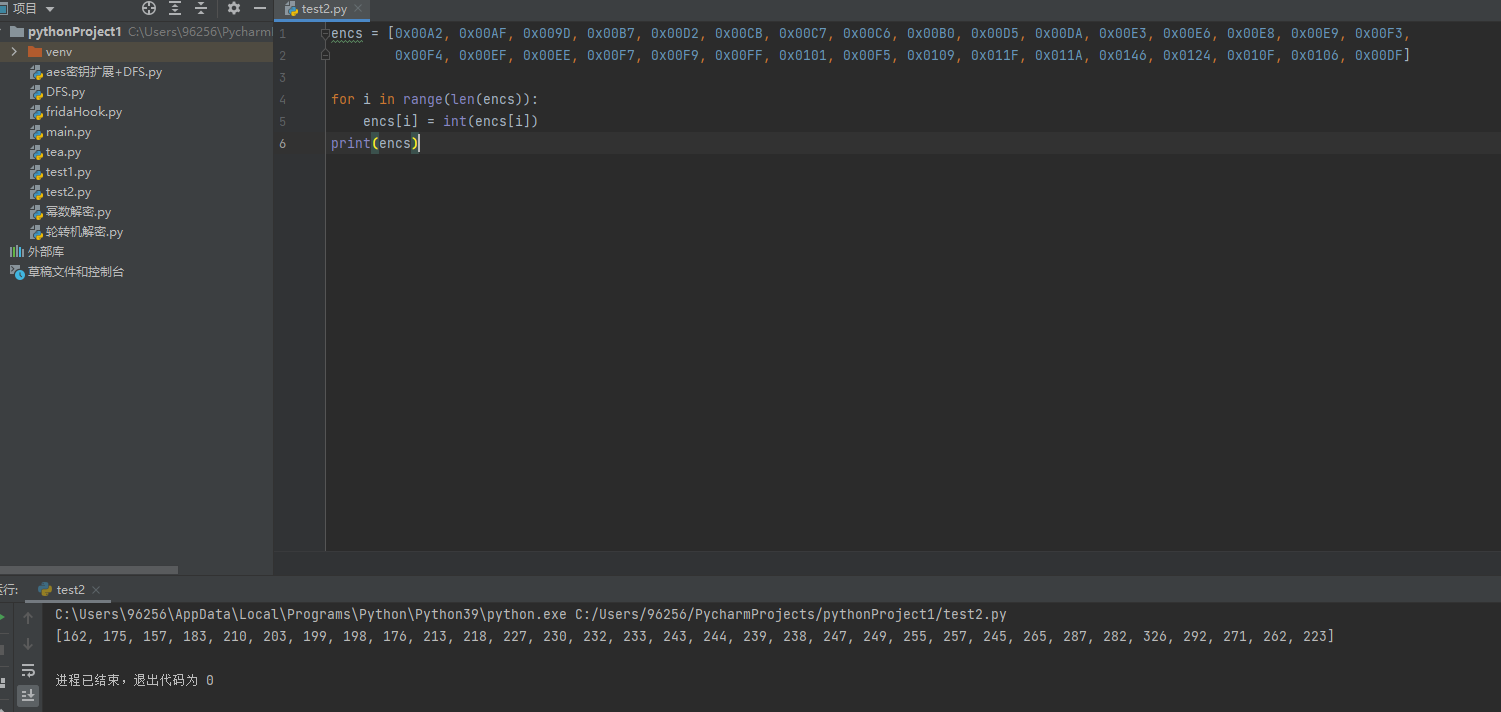

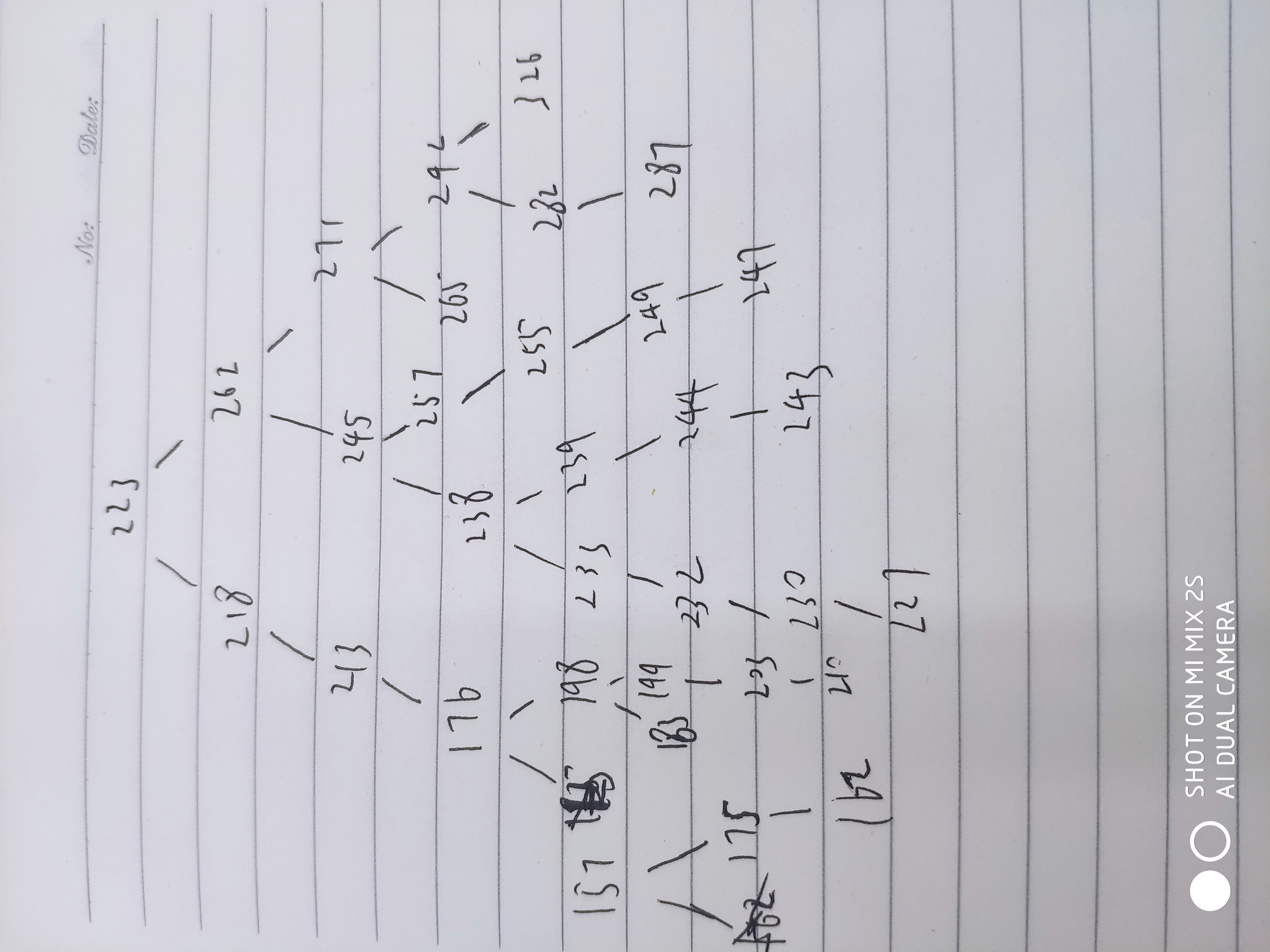
手绘了一张二叉树图 因为是后序遍历 大家可以看这张图非常直观

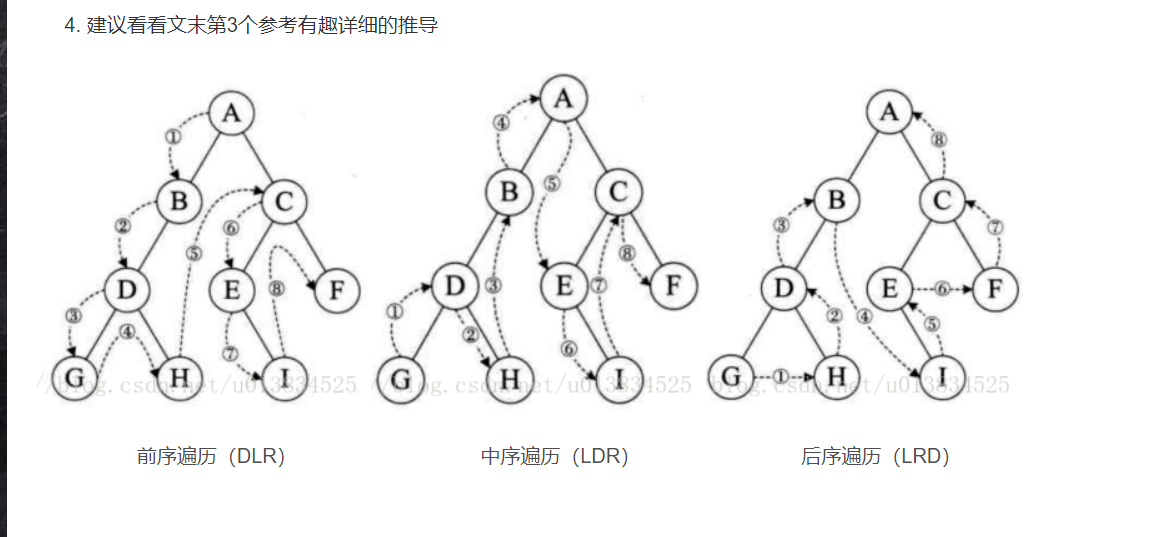
DLR–前序遍历（根在前，从左往右，一棵树的根永远在左子树前面，左子树又永远在右子树前面 ）

LDR–中序遍历（根在中，从左往右，一棵树的左子树永远在根前面，根永远在右子树前面）

LRD–后序遍历（根在后，从左往右，一棵树的左子树永远在右子树前面，右子树永远在根前面）

再加上 上方的叶子个数可以画出这个图

0x6最终的动调

会发现 除了对比加密后的flag 还会对比左孩子右兄弟 错误直接退出

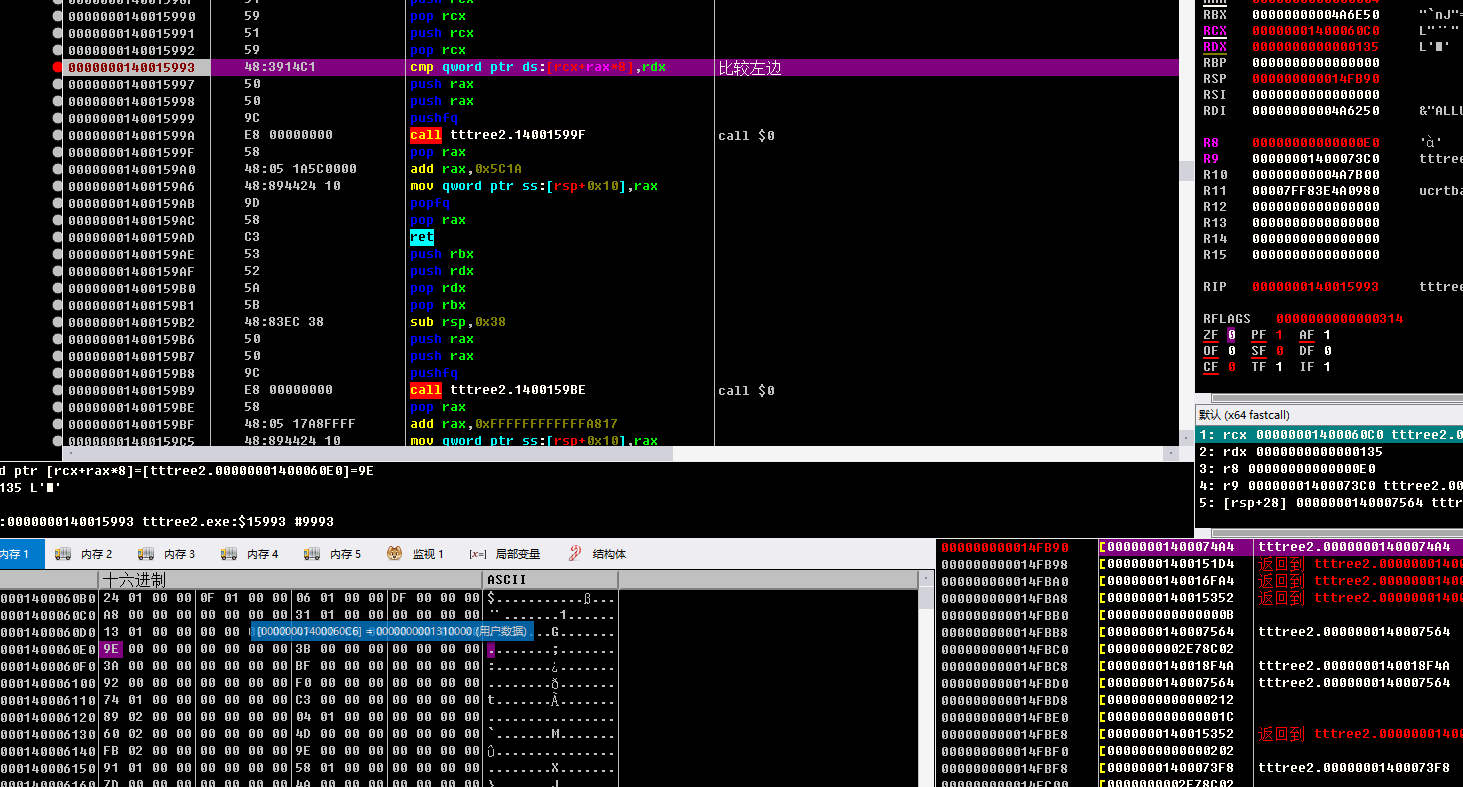
提取里面的对比值

gxs_right = [0x00AC, 0x00FD, 0x0247, 0x0115, 0x00D4, 0x02B5, 0x01FC, 0x028B, 0x014A, 0x004C, 0x008E, 0x00E9, 0x0055, 0x012C, 0x00F5,
             0x00E3, 0x0081, 0x02E2, 0x01A8, 0x0117, 0x0152, 0x0101, 0x003A, 0x01D0, 0x00A8, 0x00CC, 0x0149, 0x0137, 0x0300, 0x01EC, 0x0276, 0x0247]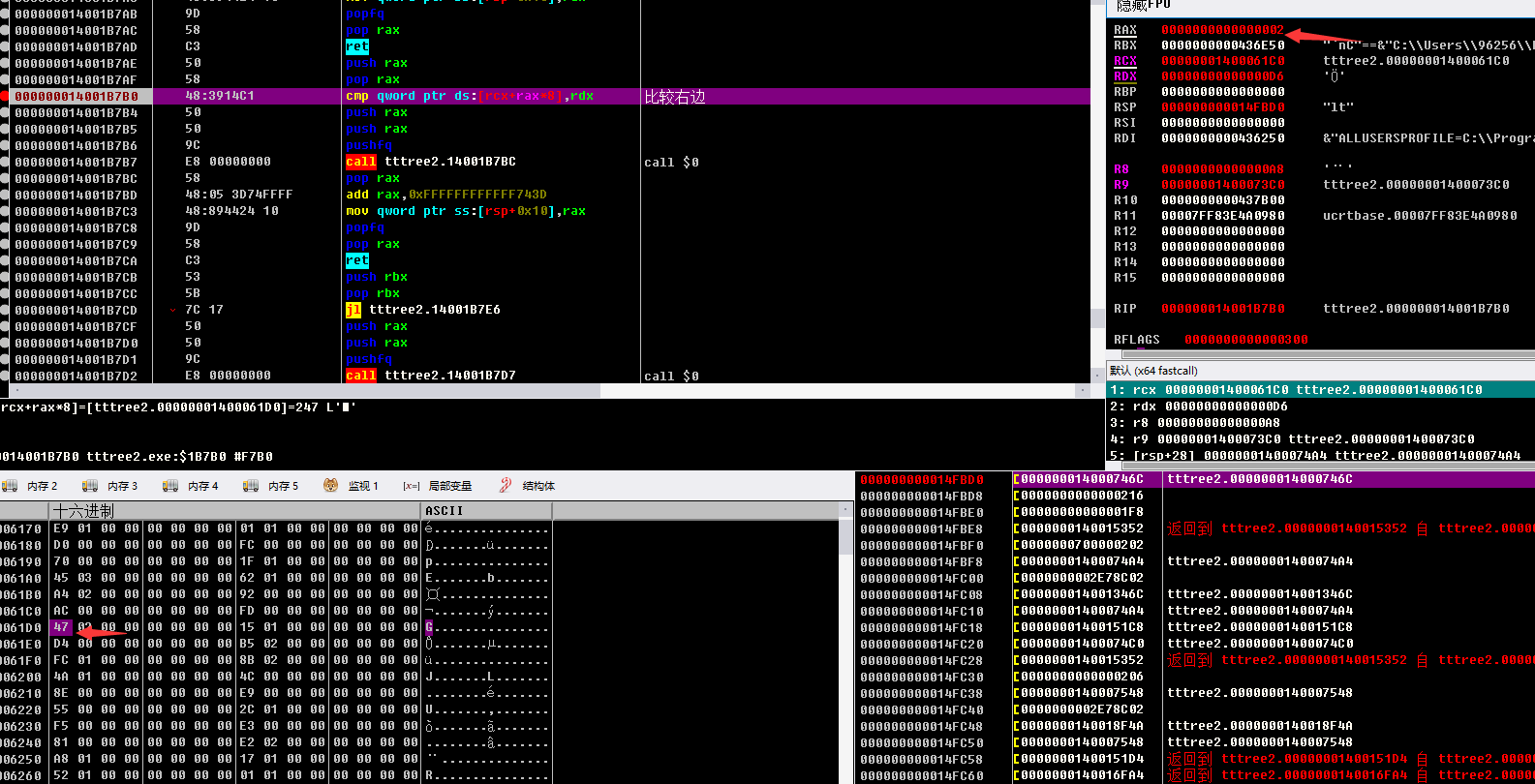

gxs_left = [0x00A8, 0x0131, 0x0113, 0x0047, 0x009E, 0x003B, 0x003A, 0x00BF, 0x0092, 0x00F0, 0x0174, 0x00C3, 0x0289, 0x0104, 0x0260,
            0x004D, 0x02FB, 0x009E, 0x0191, 0x0158, 0x007D, 0x004A, 0x01E9, 0x0101, 0x00D0, 0x00FC, 0x0070, 0x011F, 0x0345, 0x0162, 0x02A4, 0x0092]

0x7编写解密脚本

因为Treap有堆的性质，根节点的优先级是最小的，因此我们提取出所有的优先级，对他进行排序

所以可以得到后序遍历最终顶端的值 后面就不行，分支下去后就有两个 优先级无法判定

c = [0x2109B018, 0x11BB2E13, 0x5D64CABB, 0x302F1C09, 0x02E78C02, 0x2A28B165, 0x6F018185, 0x1CF5A8D1, 0x1532F368, 0x42367652, 0x7B50B157, 0x244FA941, 0x48CB7CCC, 0x1950F130, 0x15561F1B, 0x29F35383,
     0x204017F9, 0x15686F99, 0x274AD200, 0x650387E1, 0x04C2B77D, 0x278451D6, 0x3F0318C0, 0x78E83012, 0x0D00C42A, 0x537C7E9D, 0x0F8680AF, 0x72A27C9F, 0x5C4909AF, 0x2FE974B3, 0x351BEA91, 0x2ADAD13B]
yxj = [[i, c[i]] for i in range(len(c))]

def sort_(elem):
    return elem[1]

yxj.sort(key=sort_)
print(yxj)
# [[4, 48729090], [20, 79869821], [24, 218154026], [26, 260473007], [1, 297479699], [8, 355660648], [14, 357965595], [17, 359165849], [13, 424735024], [7, 485861585], [16, 541071353], [0, 554283032], [11, 609200449], [18, 659214848], [21, 662983126], [15, 703812483], [5, 707309925], [31, 718983483], [29, 803828915], [3, 808393737], [30, 891021969], [22, 1057167552], [9, 1110865490], [12, 1221295308], [25, 1400667805], [28, 1548290479], [2, 1566886587], [19, 1694730209], [6, 1862369669], [27, 1923251359], [23, 2028482578], [10, 2068885847]]

可以发现，索引是4，即序号是5的时候最小，即223的序号是5，根据5(序号)和223(enc_input)进行解密就可以得到本节点字符 ‘d’

def get_real_c(_index, enc_input):
    # 通过索引和enc_input得到原始input
    tmp = enc_input - 97 - key[_index] - _index
    return tmp

get_real_c(4, 223)
# 100 -->chr(100) = 'd'

# [本节点，左孩子，右孩子，序号，flag]
# 构造二叉树
treap = [
    [223, 218, 262, 5, 100],
    [218, 213, 0, 0, 0],
    [213, 176, 0, 0, 0],
    [176, 157, 198,  0, 0],
    [157, 0, 175, 0, 0],
    [175, 162, 0, 0, 0],
    [198, 183, 199, 0, 0],
    [162, 0, 0, 0, 0],
    [183, 0, 0, 0, 0],
    [199, 0, 203, 0, 0],
    [203, 0, 210, 0, 0],
    [210, 0, 0, 0, 0],
    [262, 245, 271, 0, 0],
    [245, 238, 257, 0, 0],
    [238, 233, 239, 0, 0],
    [233, 232, 0, 0, 0],
    [232, 230, 0, 0, 0],
    [230, 227, 0, 0, 0],
    [227, 0, 0, 0, 0],
    [239, 0, 244, 0, 0],
    [244, 243, 0, 0, 0],
    [243, 0, 0, 0, 0],
    [257, 255, 0, 0, 0],
    [255, 249, 0, 0, 0],
    [249, 247, 0, 0, 0],
    [247, 0, 0, 0, 0],
    [271, 265, 292, 0, 0],
    [265, 0, 0, 0, 0],
    [292, 282, 326, 0, 0],
    [282, 0, 287, 0, 0],
    [326, 0, 0, 0, 0],
    [287, 0, 0, 0, 0]
]

treap_dict = {}
for i in range(32):
    treap_dict[treap[i][0]] = treap[i][1:5]   #提取除了本节点外的另外4个值
key = [0x60, 0x46, 0x62, 0x03, 0x16, 0x19, 0x1E, 0x12, 0x4D, 0x51, 0x05, 0x25, 0x38, 0x2F, 0x14, 0x4F,
       0x5B, 0x2D, 0x4C, 0x26, 0x5A, 0x0F, 0x04, 0x07, 0x5F, 0x1D, 0x48, 0x1F, 0x67, 0x44, 0x3B, 0x37]  #第一次加密用的key
encs = [0x00A2, 0x00AF, 0x009D, 0x00B7, 0x00D2, 0x00CB, 0x00C7, 0x00C6, 0x00B0, 0x00D5, 0x00DA, 0x00E3, 0x00E6, 0x00E8, 0x00E9, 0x00F3,
        0x00F4, 0x00EF, 0x00EE, 0x00F7, 0x00F9, 0x00FF, 0x0101, 0x00F5, 0x0109, 0x011F, 0x011A, 0x0146, 0x0124, 0x010F, 0x0106, 0x00DF]  #最终对比的加密的值 真正的flag

# 节点和右孩子之间的关系
gxs_right = [0x00AC, 0x00FD, 0x0247, 0x0115, 0x00D4, 0x02B5, 0x01FC, 0x028B, 0x014A, 0x004C, 0x008E, 0x00E9, 0x0055, 0x012C, 0x00F5,
             0x00E3, 0x0081, 0x02E2, 0x01A8, 0x0117, 0x0152, 0x0101, 0x003A, 0x01D0, 0x00A8, 0x00CC, 0x0149, 0x0137, 0x0300, 0x01EC, 0x0276, 0x0247]

# 节点和左孩子之间的关系
gxs_left = [0x00A8, 0x0131, 0x0113, 0x0047, 0x009E, 0x003B, 0x003A, 0x00BF, 0x0092, 0x00F0, 0x0174, 0x00C3, 0x0289, 0x0104, 0x0260,
            0x004D, 0x02FB, 0x009E, 0x0191, 0x0158, 0x007D, 0x004A, 0x01E9, 0x0101, 0x00D0, 0x00FC, 0x0070, 0x011F, 0x0345, 0x0162, 0x02A4, 0x0092]

def get_child_xuhao(node_c, gx):
    # node_c： 本节点字符
    # gx: 关系
    # 孩子节点序号 * 0x17  + 本节点input = gx
    if (gx - node_c) % 0x17 == 0:
        return int((gx - node_c) / 0x17)
    return None

def get_real_c(_index, enc_input):
    # 通过索引和enc_input得到原始input
    tmp = enc_input - 97 - key[_index] - _index
    return tmp

def treap_traverse(_root):
    if _root == 0:
        return
    node_c = get_real_c(treap_dict[_root][2] - 1, _root)   #获取input的序号  例：提取了 233 的序号 5  然后减 1 为 4  因为序号5  索引为4   所以需要减一  然后解密出来
    idx = encs.index(_root)     # 得到后续遍历后的数组中_root的索引
    # 如果左节点不为空，更新左节点的数据
    left_root = treap_dict[_root][0]   #获取左孩子
    right_root = treap_dict[_root][1]   #获取右孩子
    if left_root != 0:
        left_xh = get_child_xuhao(node_c, gxs_left[idx])     #放入解密后的值 和 左孩子里索引的值  得到序号
        left_c = get_real_c(left_xh - 1, treap_dict[_root][0])     #跟上面一样  填入序号 减一  然后解密
        treap_dict[left_root][2] = left_xh              #填入序号
        treap_dict[left_root][3] = left_c               #填入解密后的值
        treap_traverse(left_root)
    if right_root != 0:
        right_xh = get_child_xuhao(node_c, gxs_right[idx])
        right_c = get_real_c(right_xh - 1, treap_dict[_root][1])     # 右孩子
        treap_dict[right_root][2] = right_xh
        treap_dict[right_root][3] = right_c
        treap_traverse(right_root)

treap_traverse(223)   #放入已知的  223  序号为5  来推导剩下的
flag = []
for _key, value in treap_dict.items():   #把序号 和 解密完的值提取出来
    flag.append([value[2], value[3]])
flag.sort()      #根据序号 排序
flag = [x[1] for x in flag]    #排序完后 只将解密的值拿出来
print("SUSCTF{" + "".join(map(chr, flag)) + "}")   #打印出来就成功啦
# SUSCTF{8226d8a68d25d8f03be17c4d7027b29c}

0x8总结

花了快一天的时间，原本不想复现这题，但是看见有人全程动调出题，就非常也想尝试一下，感觉非常累，但是经验积累了很多。（早知道理解wp的去花脚本.）

之前看过二叉树，这次感觉又重新学习了一遍，完全忘记了。 在这里感谢一下这位师傅的文章@zsky（懒的重写，理解完就注释结束了…代码基本全抄，动调提取倒是自己做的）

文章链接（https://www.52pojie.cn/thread-1596550-1-1.html）